Category: fractaluniverse

Apakah yang di Maksud Dengan Alam Semesta Fraktal – Pada suatu malam musim panas hampir 40 tahun yang lalu, Andrei Linde tiba-tiba diliputi oleh keyakinan bahwa dia tahu bagaimana alam semesta dilahirkan. Momen eureka nokturnalnya akan mengarah pada konsep multiverse, bagian sentral dari Lanskap Teori String. Cerita ini adalah bagian ke-3 dari seri lima bagian.

Pada suatu malam musim panas tahun 1981, ketika masih menjadi peneliti junior di Institut Fisika Lebedev di Moskow, Andrei Linde dikejutkan oleh sebuah wahyu. Karena tidak dapat menahan kegembiraannya, dia membangunkan istrinya, Renata Kallosh, dan berbisik kepadanya dalam bahasa Rusia asli mereka, “Saya rasa saya tahu bagaimana alam semesta dilahirkan.”

Kallosh, yang juga seorang ahli fisika teoretis, menggumamkan beberapa kata yang memberi semangat dan kembali tertidur. https://www.americannamedaycalendar.com/

“Baru keesokan paginya saya menyadari dampak penuh dari apa yang dikatakan Andrei kepada saya,” kenang Kallosh, yang sekarang menjadi profesor fisika di Institut Fisika Teoritis Stanford.

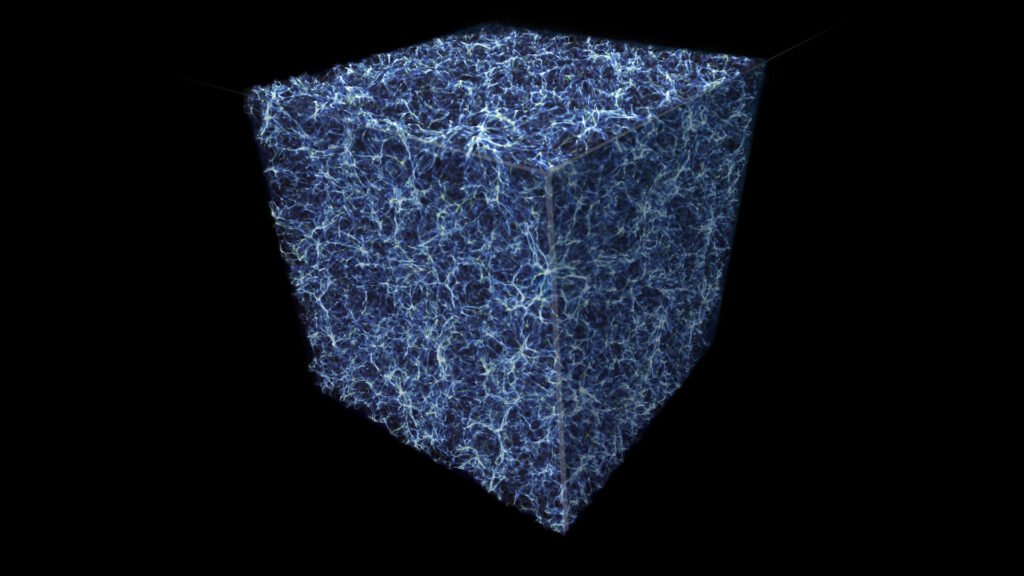
Momen eureka nokturnal Linde berkaitan dengan masalah dalam kosmologi yang ia dan para ahli teori lainnya, termasuk Stephen Hawking, perjuangkan selama berbulan-bulan.

Terowongan

Untuk menyimpulkan pembongkaran ruang-waktu, Guth meminjam sebuah trik dari mekanika kuantum yang disebut “tunneling” yang memungkinkan medan inflasinya berpindah secara acak dan instan dari keadaan energi yang lebih tinggi dan kurang stabil ke keadaan energi yang lebih rendah, sehingga melewati penghalang yang tidak bisa. dapat diskalakan oleh fisika klasik.
Namun pengamatan lebih dekat mengungkapkan bahwa terowongan kuantum menyebabkan medan inflasi meluruh dengan cepat dan tidak merata, sehingga menghasilkan alam semesta yang tidak datar dan tidak seragam. Sadar akan kelemahan fatal dalam teorinya, Guth menulis di akhir makalahnya tentang inflasi: “Saya menerbitkan makalah ini dengan harapan akan… mendorong orang lain untuk menemukan cara menghindari hal-hal yang tidak diinginkan dalam skenario inflasi.”

Kelahiran kuantum galaksi

Pada saat Linde dan Kallosh pindah ke Stanford pada tahun 1990, eksperimen mulai mengejar teori tersebut. Misi luar angkasa menemukan variasi suhu dalam pancaran energi Big Bang – yang disebut radiasi latar gelombang mikro kosmik – yang mengkonfirmasi prediksi mengejutkan yang dibuat oleh model inflasi terbaru.

Model-model yang diperbarui ini memiliki berbagai nama – “inflasi kacau”, “inflasi abadi”, “inflasi kacau abadi”, dan masih banyak lagi – namun semuanya memiliki kesamaan yaitu jalan keluar yang mulus seperti yang dirintis Linde.

Multiverse

Linde dan yang lainnya kemudian menyadari bahwa fluktuasi kuantum yang sama yang menghasilkan galaksi dapat menimbulkan wilayah penggembungan baru di alam semesta. Meskipun inflasi sudah berakhir di lingkungan kosmik lokal kita 14 miliar tahun yang lalu, inflasi masih dapat berlanjut di pinggiran terluar alam semesta. Konsekuensinya adalah lautan ruang-waktu yang semakin membesar dan dipenuhi dengan “alam semesta pulau” atau “alam semesta saku” seperti alam semesta kita, di mana inflasi telah berhenti. “Akibatnya, alam semesta menjadi multiverse, sebuah fraktal yang terus tumbuh dan terdiri dari banyak bagian yang berukuran sangat besar secara eksponensial,” tulis Linde. “Bagian-bagian ini begitu besar sehingga dalam praktiknya mereka terlihat seperti alam semesta yang terpisah.”

Linde membawa gagasan multiverse lebih jauh lagi dengan mengusulkan bahwa setiap alam semesta saku bisa mempunyai sifat yang berbeda-beda, sebuah kesimpulan yang juga dicapai oleh beberapa ahli teori string secara independen. “Bukan karena hukum fisika di setiap alam semesta berbeda, tapi realisasinya,” kata Linde. “Analoginya adalah hubungan antara air cair dan es. Keduanya adalah H2O tetapi diwujudkan secara berbeda.”

Menyelami Lebih Dalam Alam Semesta Ketakterhinggaan Fraktal – Alam menampakkan dirinya dalam keadaan linglung. Cabang-cabang pepohonan terbelah dengan hiruk pikuk, ombak laut menerjang tepian pantai. Di atas kita, abu bintang berkumpul membentuk konstelasi baru. Di bawah kita, koloni bakteri berpindah ke hutan mikroba yang subur. Dalam kehidupan kita sendiri, kita terbiasa dengan spontanitas ketika kita hanyut mengikuti arus momen saat ini. Semuanya berubah-ubah, seiring kekacauan kekuatan yang menjerat alam semesta kita.

Meskipun entropi memberi tahu kita bahwa alam semesta akan mengalami kekacauan dalam jangka panjang, terdapat keteraturan aneh yang mendasari dinamika kompleksnya. Pola-pola alam yang aneh ini muncul di setiap sudut. Mereka kecil, namun lebih besar dari kehidupan; mereka abadi, namun segar. Ini adalah lubang intip kaleidoskopik yang melaluinya kita dapat mengamati cara kerja alam semesta. Masukkan, fraktal.

Apa itu Fraktal?

Fraktal tampak seperti paradoks: luar biasa namun tersembunyi di depan mata, bentuk-bentuk berpola ini menunjukkan tingkat kerumitan yang tak ada habisnya. Anda mungkin mengenalnya sebagai bangun datar yang luasnya terbatas tetapi kelilingnya tidak terbatas. www.mrchensjackson.com

Fraktal mengungkapkan hal ini melalui properti khusus yang disebut kesamaan diri, artinya memperbesar bagian mana pun dari fraktal dapat membuat Anda melihat replika keseluruhannya. Kesamaan diri memberi fraktal kualitas yang tampak terfragmentasi dan tidak beraturan, namun dalam arti lain, fraktal berbentuk geometris yang unik.

Menariknya, seluk-beluk fraktal dapat ditangkap dengan mengulangi algoritma sederhana dalam proses yang dikenal sebagai rekursi, dimana hasil dari satu generasi merupakan puncak dari generasi sebelumnya. Lihatlah sebuah pohon. Pertama, Anda melihat jangkauan bagasi yang luas. Kemudian Anda melihat cabang-cabang besar tumbuh dari batangnya. Cabang-cabang yang besar ini menghasilkan ranting-ranting yang lebih kecil dari dahan-dahan tersebut, yang kemudian menghasilkan ranting-ranting yang lebih kecil lagi, dan seterusnya. Dengan setiap pembesaran pada pohon, cabang-cabang yang semakin halus muncul hingga sebelas urutan cabang.

Pola fraktal dapat dibuat dengan pensil dan kertas. Misalnya, jika Anda berulang kali membagi sebuah segitiga menjadi bagian-bagian yang semakin kecil, Anda akan mendapatkan Segitiga Sierpiński yang bergerigi tipis. Atau, dengan terus-menerus menggambar segitiga-segitiga yang lebih kecil dan lebih kecil yang memanjang dari segitiga alasnya, Anda akan mendapatkan bentuk yang sangat mirip dengan kepingan salju, yang umumnya dikenal sebagai Kepingan Salju Koch.

Menemukan Fraktal

Berbagai budaya di seluruh dunia telah lama terpikat oleh sifat fraktal dari realitas. Fraktal telah memberi mandala makna spiritual dalam agama Buddha dan mengekspresikan keanggunan surgawi dalam arsitektur Gotik. Mulai dari tesselasi rumit yang menghiasi masjid-masjid Islam hingga desain karpet Persia yang simetris yang ditenun oleh suku nomaden. Tentu saja, seni dan budaya mencerminkan keinginan lama kita untuk meniru estetika alam.

Namun struktur fraktal yang mendasari motif-motif ini baru dapat dipahami pada akhir abad ke-20. Pada akhir tahun 70-an, matematikawan Polandia dan ahli dalam segala bidang, Benoît B. Mandelbrot, berusaha menemukan cara untuk menangkap seluk-beluk realitas yang telah membingungkan para matematikawan sebelumnya. Seperti yang diyakini Mandelbrot, garis aljabar yang kaku dan kurva kalkulus yang mulus terlalu ideal untuk dilakukan. Sebaliknya, kenyataan berada dalam kegilaan yang luar biasa, “Awan bukanlah bola, gunung bukanlah kerucut, garis pantai bukanlah lingkaran, dan kulit kayu tidak mulus, petir juga tidak merambat dalam garis lurus,” tulis Mandelbrot yang terkenal.

Flora, Fraktal, Fauna

Fraktal sangat menarik karena merupakan tulang punggung alam dalam jumlah besar. Ini adalah produk sampingan yang aneh dari hukum fisika alam semesta yang mulai membuahkan hasil. Dalam banyak kasus, hal ini terjadi karena pola fraktal merangkum cara paling efektif untuk mengefektifkan energi di seluruh ekosistem.

Kehidupan biologis memiliki banyak struktur fraktal. Lihatlah daun tanaman pakis: setiap daun adalah versi mini dari keseluruhannya. Atau Brokoli Romanesco, salah satu fraktal paling baru, yang tunas besarnya mengandung lanskap intim dari tunas kecil, dan tunas kecil ini mengandung tunas yang lebih kecil lagi, dan seterusnya. Kuntum beberapa bunga, seperti bunga matahari, disusun sepanjang spiral Fermat (sudut khusus dengan sifat rasio emas) untuk menciptakan kepala bunga spiral yang fotogenik. Struktur spiral sangat umum ditemukan, seperti yang ditemukan di atas badai topan atau struktur kerang yang melilit.

Fraktal bahkan merupakan komponen anatomi kita. Kita manusia dilahirkan dengan pembuluh darah yang terjalin rumit yang melacak seluruh volume tubuh kita. Secara keseluruhan, pembuluh darah kita membentang sepanjang 60.000 mil, namun dengan terbentuk dalam pola fraktal, tubuh kita memastikan bahwa setiap sudut dan celah tertutup untuk menjaga suhu tubuh yang optimal. Hal yang sama juga berlaku pada distribusi bronkiolus di paru-paru kita, yang meluas ke segala arah seperti akar pohon untuk memaksimalkan pertukaran gas.

Apakah Alam Semesta Itu Fraktal Raksasa ? – Fraktal adalah objek yang terlihat sama pada semua skala Saya yakin banyak dari Anda pernah melihat gambar atau video fraktal, tetapi jika belum atau ingin diingatkan, lihat representasi visual yang diposting di YouTube. Sebagai seorang kosmolog yang telah mempelajari struktur alam semesta berskala besar, saya menemukan pertanyaan apakah alam semesta itu sendiri merupakan fraktal raksasa yang cukup menarik.

Sebelum kita mendalami pertanyaan ini lebih dalam, diperlukan beberapa informasi latar belakang. Kesimpulan umum dalam kosmologi adalah bahwa Alam Semesta berasal dari Dentuman Besar (Big Bang) yang menggerakkan semua materi dan energi. Meskipun awalnya hampir seragam, gangguan kuantum kecil membuat bagian tertentu di Alam Semesta sedikit lebih padat dibandingkan bagian lainnya. https://www.mrchensjackson.com/

Ketika gravitasi mengarahkan materi ke wilayah yang terlalu padat ini, struktur perlahan mulai terbentuk. Setelah miliaran tahun, struktur ini berevolusi menjadi kumpulan besar filamen dan rongga. Video simulasi Milenium berikut ini menampilkan model struktur tersebut pada skala panjang yang berbeda.

Seperti yang diperlihatkan dalam video, Alam Semesta tampak serupa pada semua skala, kecuali skala terkecil. Bahwa Alam Semesta gagal menjadi fraktal dalam skala kecil seharusnya sudah jelas. Lagi pula, tidak ada objek seukuran galaksi yang terlihat seperti gletser, pohon, atau tupai. Oleh karena itu, jika Alam Semesta memang memiliki sifat mirip fraktal, alam semesta pasti akan terurai suatu saat nanti. Di atas skala tersebut, apakah alam semesta tampak seperti fraktal? Jika ya, apakah fraktal itu berlangsung selamanya? Kalau tidak dipotong di mana. Mengapa? Bagaimana kami bisa tahu?

Inilah pertanyaan yang saya selidiki dalam posting ini. Peringatan yang adil: ini akan menjadi sangat buruk. Mereka yang cukup berani untuk melanjutkan didorong untuk mengenakan topi matematika mereka.

Salah satu cara kosmolog mengukur struktur adalah melalui statistik yang dikenal sebagai fungsi korelasi dua titik (2PCF). 2PCF mengukur probabilitas f

statistik yang dikenal sebagai fungsi korelasi dua titik (2PCF). 2PCF mengukur kemungkinan ditemukannya dua galaksi yang dipisahkan oleh jarak r melebihi perkiraan melalui kebetulan acak.

Dalam tiga dimensi fungsi korelasi dua titik sering didekati sebagai hukum pangkat,

\begin{equation} \xi(r) \propto r^{-\gamma}, \end{equation}

dimana \gamma adalah parameter yang nilainya bergantung pada sebaran galaksi tertentu. Dalam dua dimensi 2PCF w(\theta) adalah fungsi sudut,

(2) \mulai{persamaan} w(\theta) \propto \theta^{-(\gamma-1)}. \end{persamaan}

Perhatikan bahwa jika kita menambahkan jumlah dimensi Euclidean1 ke eksponen 2PCF kita memperoleh angka yang sama, 3-\gamma. Ini dikenal sebagai kodimensi. Ternyata jika Anda memiliki proses acak dengan fungsi korelasi hukum pangkat, saat Anda memproyeksikannya ke dimensi yang lebih rendah, kodimensinya tidak berubah.

Untuk lebih memahami hal ini, mari kita pertimbangkan fungsi korelasi galaksi dua titik secara lebih mendalam. Untuk menghitung nilainya pada r apa pun, kami mengisi volume simulasi dengan2 titik acak yang terdistribusi secara merata. Kami menghitung jumlah pasangan titik yang dipisahkan oleh setiap jarak r dan menggunakan hasilnya untuk mengisi apa yang disebut histogram acak-acak. Kami melakukan hal yang sama pada galaksi untuk menghasilkan data-data histogram. Rasio histogram ini, yang merupakan ukuran probabilitas yang melebihi apa yang diharapkan melalui kebetulan acak, adalah 2PCF.3

Sebagai contoh, perhatikan alam semesta tiga dimensi yang seluruh galaksinya terletak pada satu garis lurus. Kita membatasi fokus kita pada galaksi-galaksi yang terpisah sejauh r dengan membayangkan cangkang bola berjari-jari r. Satu-satunya titik data-data akan terletak saling berhadapan, mungkin terletak di kutub yang berlawanan. Jumlah pasangan galaksi akan berskala 2\lambda\, dr dengan \lambda adalah kepadatan galaksi linier. Titik-titik acak dapat terletak di mana saja dalam cangkang bola, sehingga menghasilkan jumlah pasangan yang jauh lebih besar. Jumlah pasangan ini akan berskala 4\pi r^2 \rho\, dr di mana \rho adalah kepadatan volume acak.4 Fungsi korelasi kemudian akan menjadi

\begin{persamaan} \xi=\frac{2\lambda \, dr}{4\pi r^2 \rho \, dr} \propto \frac{1}{r^2}=\left( \frac {1}{r} \kanan)^{\gamma=2}. \end{persamaan}
Dengan argumen serupa, jika seluruh massa di Alam Semesta berada pada bidang datar, maka jumlah pasangan data-data adalah 2\pi r \sigma\,dr dengan \sigma adalah kepadatan area galaksi.5 Dalam kasus ini, fungsi korelasi akan menjadi

(4) Mulailah dengan persamaan: xi=frac{2\pi r sigma,dr}{4\pi r^2 ho, dr} dan frac{1}{r}=kiri(frac{1}{r}kanan)^{gamma=1}. Terakhir, persamaan*.
Kodimensi alam semesta linier adalah 3-\gamma=1. Kodimensi alam semesta planar adalah 2.

Alasan mengapa hal ini penting adalah karena proses acak (seperti distribusi galaksi) dengan fungsi korelasi hukum pangkat memiliki banyak kesamaan dengan fraktal.6 Untuk mengetahui caranya, mari kita periksa konsep dimensi dengan lebih teliti.

Apakah Alam Semesta Sebenarnya Merupakan Fraktal? – Jika Anda melihat struktur yang terbentuk di Alam Semesta, banyak hal yang kita lihat dalam skala besar juga muncul dalam skala yang lebih kecil. Lingkaran cahaya materi gelap di sekitar struktur terikat terbesar yang kita ketahui mirip dengan gumpalan substruktur kecil di sekitar galaksi yang lebih kecil dan di ruang antargalaksi. Gravitasi adalah satu-satunya gaya yang signifikan pada skala terbesar di alam semesta. Dalam banyak keadaan, jika Anda menunggu cukup lama, keruntuhan gravitasi akan menghasilkan struktur yang identik, hanya saja ukurannya diperbesar atau diperkecil tergantung pada ukuran sistem Anda.

Gagasan bahwa pada akhirnya Anda akan menemukan struktur yang mengulangi pola pertama yang Anda lihat pada skala yang lebih besar, secara matematis diwujudkan dalam konsep fraktal. Ketika pola serupa muncul pada skala yang semakin kecil berulang kali, kita dapat menganalisisnya secara matematis untuk melihat apakah pola tersebut memiliki karakteristik statistik yang sama dengan struktur yang sama. lebih besar; jika ya, sifatnya seperti fraktal. Jadi, apakah alam semesta itu sendiri merupakan fraktal? www.benchwarmerscoffee.com

Secara matematis, sebagian besar dari kita terbiasa dengan bilangan real: bilangan yang dapat dinyatakan dalam format desimal, meskipun desimal tersebut panjangnya tak terhingga dan meskipun tidak pernah berulang.

Namun ada lebih banyak bilangan yang ada secara matematis daripada bilangan riil; misalnya ada bilangan kompleks. Bilangan kompleks mempunyai bagian real dan juga bagian imajiner, yaitu bilangan real dikalikan i, yang didefinisikan sebagai akar kuadrat dari -1. Angka-angka tersebut mencakup bilangan real, namun membawa kita melampaui batasan bekerja hanya dengan bilangan real saja.

Himpunan Mandelbrot adalah fraktal yang paling terkenal, yang digambarkan pada diagram di atas dan video di bawah dalam bidang kompleks, di mana sumbu x adalah nyata dan sumbu y adalah imajiner. Cara kerja himpunan Mandelbrot adalah dengan mempertimbangkan setiap kemungkinan bilangan kompleks, n, lalu melihat barisan berikut:

Cara memvisualisasikan himpunan Mandelbrot adalah dengan merepresentasikan batas antara apa yang sebenarnya ada di dalam himpunan dengan apa yang ada di luarnya, dengan kode warna yang menunjukkan seberapa jauh suatu jarak untuk menjadi anggota himpunan tersebut. (Warna-warna cerah semakin dekat dengan warna tersebut.) Seperti yang Anda lihat, banyak pola yang muncul bersifat rumit dan berulang.

Saat Anda melihat wilayah kecil yang memiliki properti yang benar-benar identik dengan keseluruhan himpunan itu sendiri, kami menyebut wilayah tersebut “serupa”. Jika sesuatu mempunyai sifat-sifat yang hampir sama dengan himpunan yang lebih besar tetapi dengan perbedaan yang tidak kentara, maka ia menunjukkan kemiripan-diri yang semu, namun jika wilayah yang kecil mempunyai sifat-sifat yang benar-benar identik dengan wilayah yang lebih besar, maka ia menunjukkan kemiripan-diri yang sesungguhnya.

Dalam himpunan Mandelbrot, Anda dapat mengidentifikasi banyak wilayah yang menunjukkan kemiripan diri semu (yang lebih umum) dan kesamaan diri sejati (yang kurang umum, namun tetap ada). Kami telah menunjukkan hal ini secara matematis pada skala yang mencakup ratusan kali lipat, jauh lebih besar daripada skala fisik yang membawa kita dari jarak terkecil antara subatom hingga seluruh Alam Semesta yang dapat diamati.

Dari sudut pandang matematis, Anda dapat melihat dengan jelas bahwa jika aturan dan ketentuan yang sama berlaku di semua skala, maka bergantung pada aturan apa yang berlaku, Anda mungkin akan mendapatkan struktur yang mirip dengan Alam Semesta, di mana apa yang muncul di skala besar juga akan sama. muncul dalam skala kecil. Ini adalah pertanyaan yang menarik perhatian pada akhir abad ke-20, ketika kita menyadari dua fakta secara bersamaan tentang kosmos.

Alam semesta, secara keseluruhan, tampaknya memiliki sejumlah besar massa yang tidak terlihat dan tidak terlihat: apa yang kita kenal sekarang sebagai materi gelap.
Kelengkungan spasial keseluruhan Alam Semesta konsisten dengan sifat datarnya, artinya jika Anda menjumlahkan semua bentuk energi yang ada di Alam Semesta, maka kepadatan kritisnya akan sama, sehingga menentukan laju ekspansi (antara lain).
Kita tahu dalam bidang fisika, astrofisika, dan kosmologi bahwa kita tidak dapat dengan tepat mensimulasikan seluruh alam semesta. Yang bisa kita lakukan adalah menyederhanakan asumsi-asumsi, lalu menyimulasikan alam semesta dengan kemampuan terbaik kita berdasarkan asumsi-asumsi tersebut. Salah satu hal menarik yang mulai kami lakukan adalah menjalankan simulasi materi gelap di Alam Semesta dalam berbagai skala.

Ahli Astrofisika, Apakah di Alam Semesta Terdapat Pola? – Paul M. Sutter adalah ahli astrofisika di SUNY Stony Brook dan Flatiron Institute, pembawa acara Ask a Spaceman dan Space Radio, dan penulis How to Die in Space.

Selama beberapa dekade, para kosmolog bertanya-tanya apakah struktur alam semesta berskala besar adalah sebuah fraktal – yaitu, apakah ia terlihat sama tidak peduli seberapa besar skalanya. Setelah menyelesaikan survei besar-besaran terhadap galaksi, para ilmuwan akhirnya mendapatkan jawabannya: Tidak, tapi bisa dibilang, bisa dibilang begitu.

Pada awal abad ke-20, para astronom – dimulai dengan Edwin Hubble dan penemuannya tentang jarak yang sangat jauh dari Andromeda, galaksi terdekat dengan Bima Sakti kita – mulai menyadari bahwa alam semesta sangatlah luas. Mereka juga mengetahui bahwa kita dapat melihat galaksi-galaksi tersebar, baik yang dekat maupun yang jauh. https://www.benchwarmerscoffee.com/

Jadi, tentu saja, timbul pertanyaan: Apakah ada pola tertentu dalam susunan galaksi-galaksi tersebut, atau justru acak?

Pada awalnya, itu tampak acak. Para astronom melihat gugus galaksi raksasa, masing-masing berisi seribu galaksi atau lebih. Dan ada juga kelompok galaksi yang jauh lebih kecil dan galaksi-galaksi yang berkumpul sendiri-sendiri. Secara keseluruhan, pengamatan tersebut membuat seolah-olah tidak ada pola menyeluruh pada kosmos.

Dan para astronom setuju dengan hal itu. Mereka telah lama mengasumsikan gagasan yang disebut prinsip kosmologis — yaitu, bahwa alam semesta sebagian besar bersifat homogen (kira-kira sama dari satu tempat ke tempat lain) dan isotropik (kira-kira sama ke arah mana pun Anda melihat). Sekumpulan galaksi dan gugus acak cocok dengan prinsip tersebut.

Namun pada akhir tahun 1970-an, survei galaksi menjadi cukup canggih untuk mengungkap awal mula pola susunan galaksi. Selain gugus, terdapat juga galaksi filamen yang panjang dan tipis. Ada tembok lebar. Dan kemudian ada kekosongan – hamparan luas yang tidak ada apa-apanya. Para astronom menyebutnya jaringan kosmik. Pola ini melanggar prinsip kosmologis, karena berarti wilayah luas di alam semesta tidak terlihat seperti wilayah besar lainnya di alam semesta.

Alam semesta di dalam alam semesta

Salah satu usulan datang dari ahli matematika Benoit Mandelbrot, bapak fraktal. Fraktal sangat sulit untuk didefinisikan, namun cukup sederhana untuk dipahami secara intuitif: Fraktal adalah pola yang berulang tidak peduli seberapa jauh Anda memperbesar atau memperkecil. Mandelbrot tidak menemukan konsep fraktal – ahli matematika telah mempelajari pola kemiripan diri selama berabad-abad – namun dia menciptakan kata “fraktal” dan mengantarkan kita pada studi modern tentang konsep tersebut.

Fraktal ada dimana-mana. Anda memperbesar titik kepingan salju, Anda akan melihat kepingan salju mini. Jika Anda memperbesar cabang-cabang pohon, Anda akan melihat miniatur cabang-cabangnya. Jika Anda memperbesar garis pantai, Anda akan melihat garis pantai mini. Fraktal mengelilingi kita di alam, dan matematika fraktal telah memungkinkan kita memahami beragam struktur serupa di alam semesta.

Jika fraktal ada dimana-mana, tebak Mandelbrot, mungkin seluruh alam semesta adalah fraktal. Mungkin apa yang kita lihat sebagai pola susunan galaksi adalah langkah awal dari fraktal terbesar yang mungkin ada. Mungkin jika kita melakukan survei yang cukup canggih, kita akan menemukan struktur yang bersarang — jaringan kosmik di dalam jaringan kosmik, memenuhi seluruh alam semesta hingga tak terbatas.

Dihomogenisasi dan dipasteurisasi

Ketika para astronom menemukan lebih banyak tentang jaringan kosmik, mereka belajar lebih banyak tentang sejarah Big Bang, dan mereka menemukan cara untuk menjelaskan keberadaan pola skala besar di alam semesta. Teori-teori tersebut meramalkan bahwa alam semesta masih homogen, hanya saja dalam skala yang jauh lebih besar daripada yang pernah diamati para astronom sebelumnya.

Ujian akhir dari alam semesta fraktal baru akan terjadi pada abad ini, ketika survei yang benar-benar raksasa, seperti Sloan Digital Sky Survey, telah mampu memetakan lokasi jutaan galaksi, melukiskan potret jaringan kosmik pada skala yang belum pernah diamati. sebelum.

Jika gagasan alam semesta fraktal benar, maka kita akan melihat jaringan kosmik lokal kita tertanam di dalam jaringan kosmik yang jauh lebih besar. Jika hal ini salah, maka pada titik tertentu, jaringan kosmik akan berhenti menjadi jaringan kosmik, dan bongkahan alam semesta yang acak dan cukup besar akan terlihat (secara statistik) seperti bongkahan acak lainnya.